The KL Divergence could be computed as follows:

where P(X) is the true distribution we want to approximate, Q(X) is the approximate distribution.
However, there are two kinds of KL Divergences: Forward and Reverse.
KL Divergence Forward: DKL(p(x)||q(x))
KL Divergence Reverse: DKL(q(x)||p(x))
KL Divergence can be used as a loss function to minimize in deep learning model. However, which KL Divergence shoud be selected in our application?
The difference between DKL(p(x)||q(x)) and DKL(q(x)||p(x)).
As to DKL(p(x)||q(x)), we must know:
when p(x) = 0, DKL(p(x)||q(x))= 0; q(x) = 0, DKL(q(x)||p(x)) =∞
Let’s see some visual examples.
There are two probability distributions and
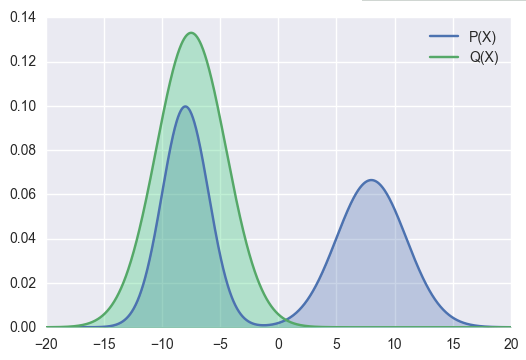
As to KL Divergence Forward, we use Q(x) to approximate P(x). The right part of P(x) > 0
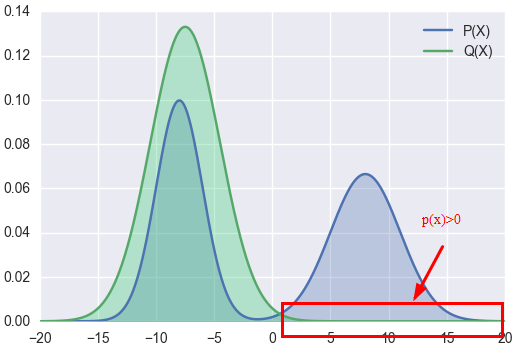
At this part, to make the kl value is minimum, the final Q(x) may be:
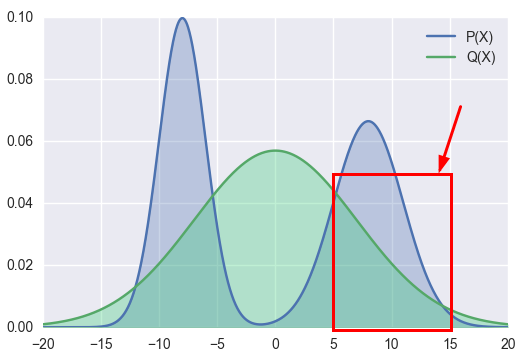
As to KL Divergence Reverse, we use P(x) to approximate Q(x). The right part of Q(x) =0
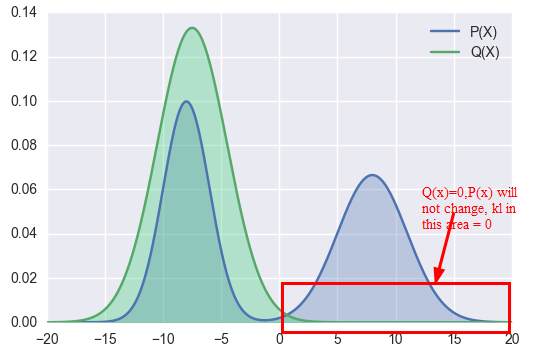
So the value of P(x) in right part will not be changed, Kl value in this area is o no matter what value of P(x) .
To make KL value is minimum, the P(x) will be like

Which one should be selected?
It depends on your problem.
In Bayesian Inference, esp. in Variational Bayes, Reverse KL is widely used. As we could see at the derivation of Variational Autoencoder, VAE also uses Reverse KL (as the idea is rooted in Variational Bayes!).
https://wiseodd.github.io/techblog/2016/12/21/forward-reverse-kl/
http://timvieira.github.io/blog/post/2014/10/06/kl-divergence-as-an-objective-function/