Implement Scale-invariant Source-to-noise Ratio (SI-SNR) in TensorFlow

Scale-invariant Source-to-noise Ratio (SI-SNR) is proposed in paper: TASNET: TIME-DOMAIN AUDIO SEPARATION NETWORK FOR REAL-TIME, SINGLE-CHANNEL SPEECH SEPARATION. In this tutorial, we will introduce how to implement it using tensorflow.

SI-SNR

SI-SNR is defined as:

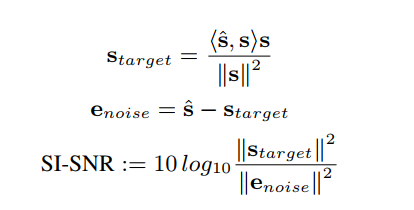
We can find and \(\hat{s}\) and \(s\) are both normalized to have zero-mean to ensure scale-invariance.

How to implement SI-SNR in tensorflow?

We will use an example to show you how to implement it.

Step 1: Create a true target and estimated target.

import tensorflow as tf
import numpy as np

EPS=1e-8

targets = tf.get_variable(shape = [16, 256], dtype=tf.float32, name = "targets")
est_targets = tf.get_variable(shape = [16, 256], dtype=tf.float32, name = "est_targets")

Here targets is our true target labels, est_targets is generated by your model.

Step 2: compute \(\hat{s}\) and \(s\)

We will compute them based on targets and est_targets.

#step 1: normalized to have zero-mean
s_target = targets - tf.reduce_mean(targets, axis = -1, keepdims = True)
s_estimate = est_targets - tf.reduce_mean(est_targets, axis = -1, keepdims = True)

Step 2: We will compute \(s_{target}\)

We should notice \(<\hat{s},s>\) is multiply and sum operation. For example:

#<s',s>
pair_wise_dot = tf.reduce_sum(s_target * s_estimate, axis = -1, keepdims = True)

Then we can compute \(s_{target}\).

s_target_energy = tf.reduce_sum(s_target ** 2, axis = -1, keepdims=True) + EPS
pair_wise_proj = pair_wise_dot * s_target / s_target_energy

Step 3: compute \(e_{noise}\)

Here is the code:

#step 2:
e_noise = s_estimate - pair_wise_proj

Step 4: compute si_snr

The code is below:

pair_wise_sdr = tf.reduce_sum(pair_wise_proj ** 2, axis=-1) / (tf.reduce_sum(e_noise ** 2, axis=-1) + EPS)

si_snr = 10 * log10(pair_wise_sdr + EPS)

Here we use a log10(x) function, you can find it in this tutorial:

Implement TensorFlow log10 Function: A Step Guide – TensorFlow Tutorial

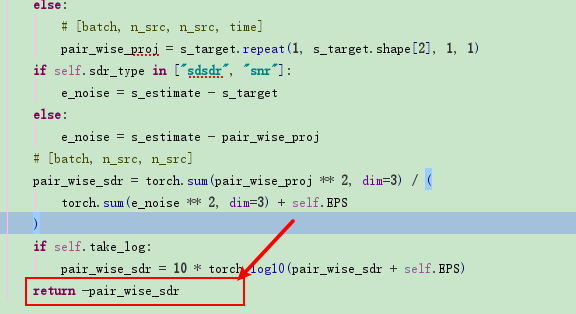
Finally,we get the si_snr. However, we should notice some model may use:

si_snr = -1.0* si_snr

For example, in python asteroid, si_snr is: