Implement Squeeze-and-Excitation (SE) Block for 2D Matrix in PyTorch – PyTorch Tutorial

As to 2D matrix, it means the shape is [batch, channel, height, width]. In this tutorial, we will introduce how to implement a squeeze-and-excitation (SE) block for this kind of data.

Squeeze-and-Excitation (SE) Block

In order to implement a se block, we can see this image:

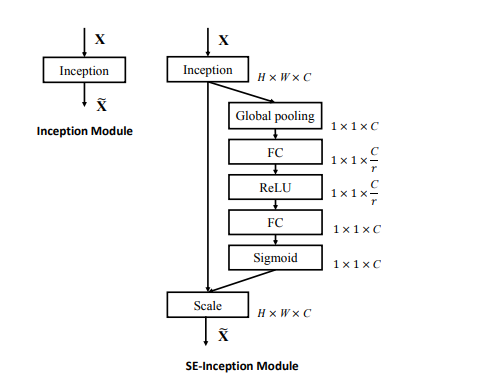
Here is a global pooling operation. We can use F.avg_pool2d() or nn.AdaptiveAvgPool2d(1) to do in pytorch.

Understand torch.nn.AdaptiveAvgPool2d() with Examples – PyTorch Tutorial

How to implement SE block for 2D matrix in pytorch?

Here is an example code:

import torch
import torch.nn as nn
import torch.nn.functional as F

class SqueezeBlock(nn.Module):
    def __init__(self, C, divide=4):
        super(SqueezeBlock, self).__init__()
        self.dense = nn.Sequential(
            nn.Linear(C, C // divide),
            nn.ReLU(inplace=True),
            nn.Linear(C // divide, C),
            nn.Sigmoid()
        )

    def forward(self, x):
        batch, channels, height, width = x.size()
        out = F.avg_pool2d(x, kernel_size=[height, width]).view(batch, -1)
        # also nn.AdaptiveAvgPool2d(1)
        print(out.shape)
        out = self.dense(out)
        out = out.view(batch, channels, 1, 1)
        return out * x

Then, we can use it as follows:

batch_size = 32
H = 20
W = 30
C = 80
se = SqueezeBlock(C)
inputs = torch.randn(batch_size, C, H, W)
outputs = se(inputs)
print(outputs.shape)

Run this code, we will see:

torch.Size([32, 80])
torch.Size([32, 80, 20, 30])