Perceptron is usually defined as:
\(y = f(W^Tx+b)\)
where \(x\) is the samples, \(W\) is the weight matrix , \(b\) is the bias vector , \(f\) is an activation function (e.g. ReLU, Tanh, Sigmoid).
This kind of perceptron can be viewed as static perceptron, Because the value of \(y\) is determined by a weight matrix \(W\) and a bias vector \(b\).
However, the value of \(y\) is not stable, because the initialized value of \(W\) and \(b\) is different when you are running your application. For example, we may use tf.random_uniform(), tf.orthogonal_initializer() or tf.glorot_uniform_initializer() to initialize them, once you have run your application 5 times, the value of \(W\) and \(b\) is different each time. The final \(y\) may also different.
In order to make the value of \(y\) much stabler, we can use dynamic perceptron.
What is dynamic perceptron?
Dynamic perceptron can be defined as:
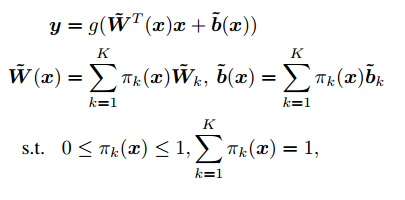
Here we have use K weights and biases to compose a perceptron. where \(\pi_k(x)\) is the attention of each perceptron.
How to compute \(\pi_k(x)\)?
You can average each perceptron and compose a perceptron, you also can use a softmax to compute weight of each perceptron.