Exponential function is defined as:
\(y = a^x\) where \(a >0\) and \(a \neq 0\).
This kind of function is widely used in machine learning. In this tutorial, we will introduce some important features when using it.
Look at image below:

1. if \(a<1\), \(b < 1\) and \(a < b\).
if \(x > 0\), then \(a^x < b^x\)
Here is an example:
\((\frac{1}{2})^{x_0}>(\frac{1}{3})^{x_0}\)
if \(x < 0\), then \(a^x > b^x\)
\((\frac{1}{2})^{x_0}<(\frac{1}{3})^{x_0}\)
2. if \(a>1\), \(b >1\) and \(a < b\).
if \(x > 0\), then \(a^x < b^x\)
\(2^{x_0}<3^{x_0}\)
if \(x < 0\), then \(a^x > b^x\)
\(2^{x_0}>3^{x_0}\)
In machine learning, decay function may use these feature. Here is an example:
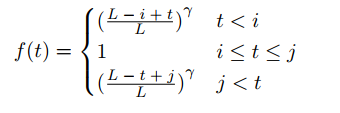
If \(\lambda\) is given. Different \(\frac{L-i+t}{L}\) will get different value.