Understand Maxout Activation Function in Deep Learning – Deep Learning Tutorial

By | March 22, 2021
0 Comment

Maxout activation functionin is proposed in paper <<Maxout Networks>>. In this tutorial, we will introduce it with some examples.

Maxout Activation Function

Maxout activation function can be defined as:

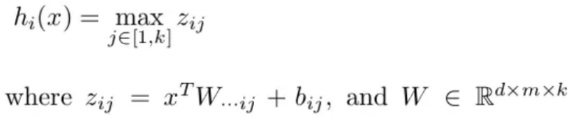
maxout activation function formula

It means we will get k maximum from \(z_1\) to \(z_k\). \(k\) is the hyper-parameter.

For example: \(x\) is a matrix with the shape d*b. As to a perceptron, we can use a \(W\) with the shape d*m to get a \(z\).

\(z = x^TW + b\)

However, if we use \(k\) projection marix \(W\) with the shape d*m*k, we will get \(k\) outputs. Then, we get the maximum for outputs, which is the maxout activation function.

For example, if \(k = 5\)

\(z1 = x^TW_1 + b_1\)

\(z2 = x^TW_2 + b_2\)

\(z3 = x^TW_3 + b_3\)

\(z4 = x^TW_4 + b_4\)

\(z5 = x^TW_5 + b_5\)

\(z = max(z1, z2, z3, z4, z5)\)

How to implement maxout activation function in tensorflow?

Here we will use an example to show you how to do.

import tensorflow as tf

x = tf.random_normal([5,3])
m = 4
k = 3
d = 3

W = tf.Variable(tf.random_normal(shape=[d, m, k])) # 3*4*3
b = tf.Variable(tf.random_normal(shape = [m, k])) # 4*3
dot_z = tf.tensordot(x, W, axes=1) + b # 5 * 4 * 3
print(dot_z)
z = tf.reduce_max(dot_z, axis=2) # 5 * 4
print(z)

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    print(sess.run([x,dot_z,z]))

Run this code, you will get this result.

Tensor("add:0", shape=(5, 4, 3), dtype=float32)
Tensor("Max:0", shape=(5, 4), dtype=float32)

[array([[ 0.54075754, -0.61821467, -1.0600331 ],
       [-2.3819177 , -1.4267262 , -0.62037367],
       [-0.9707853 ,  0.7098374 ,  0.0264655 ],
       [-2.1933246 ,  2.6150746 ,  1.3088264 ],
       [-1.1841202 ,  0.6333189 ,  0.16821939]], dtype=float32), array([[[-4.3364162e+00,  1.7406428e-01,  3.9369977e+00],
        [ 6.6635555e-01, -1.2277294e-02, -4.0200949e-03],
        [-2.7448156e+00, -9.8118293e-01,  1.0925157e+00],
        [ 1.7681911e+00, -2.5841749e+00, -8.9539540e-01]],

       [[-7.9896784e+00, -5.9510083e+00, -5.7536125e-02],
        [ 5.1459665e+00,  1.1057879e+00, -1.0491171e+00],
        [-2.3628893e+00, -1.2462056e-01,  2.1480788e-01],
        [ 4.2311554e+00, -7.2839844e-01, -3.8921905e+00]],

       [[ 6.4438421e-01, -1.1691341e+00,  6.9154239e-01],
        [ 2.9656532e-01,  1.8591885e-02, -2.2677059e+00],
        [-4.4354570e-01,  2.6578538e+00, -9.3224078e-02],
        [ 2.7506251e+00, -2.1017480e+00, -4.3397546e-01]],

       [[ 7.9296083e+00, -1.3819754e+00, -2.4889133e+00],
        [-1.2785287e+00, -2.1785280e-01, -4.9149933e+00],
        [ 2.4058640e+00,  7.1181426e+00, -1.3989885e+00],
        [ 3.4063525e+00, -1.9422388e+00,  8.8456702e-01]],

       [[ 6.0203451e-01, -1.7492318e+00,  2.8023732e-01],
        [ 5.9110224e-01,  1.2555599e-01, -2.4101894e+00],
        [-1.4339921e-01,  2.7806249e+00, -1.8500718e-01],
        [ 2.9377015e+00, -1.8836660e+00, -4.0652692e-01]]], dtype=float32), array([[ 3.9369977 ,  0.66635555,  1.0925157 ,  1.7681911 ],
       [-0.05753613,  5.1459665 ,  0.21480788,  4.2311554 ],
       [ 0.6915424 ,  0.29656532,  2.6578538 ,  2.7506251 ],
       [ 7.9296083 , -0.2178528 ,  7.1181426 ,  3.4063525 ],
       [ 0.6020345 ,  0.59110224,  2.7806249 ,  2.9377015 ]],
      dtype=float32)]

From the result, we can find:

The shape of \(x\)  is 5*3, \(W\) is 3*4*3, the output of maxout activation function is 5*4.

Leave a Reply