Cross entropy loss function is widely used in classification problem in machine learning. In this tutorial, we will discuss the gradient of it.
Cross entropy loss function
We often use softmax function for classification problem, cross entropy loss function can be defined as:

where \(L\) is the cross entropy loss function, \(y_i\) is the label.
For example, if we have 3 classes:
\(o = [2, 3, 4]\)
As to \(y = [0, 1, 0]\)
The softmax score is:
p= [0.090, 0.245, 0.665]
The cross entropy loss is:

How to compute the gradient of cross entropy loss function?
In this part, we will introduce how to compute the gradient of cross entropy loss function. As to loss function L, the gradient of \(o_k\) is computed as:
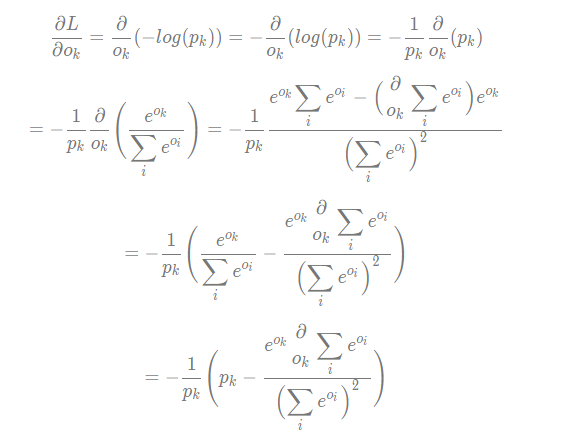
Here k is the correct class, the gradient of it is:

However, as to \(o_j\), it is not a correct class. The gradient of it is:
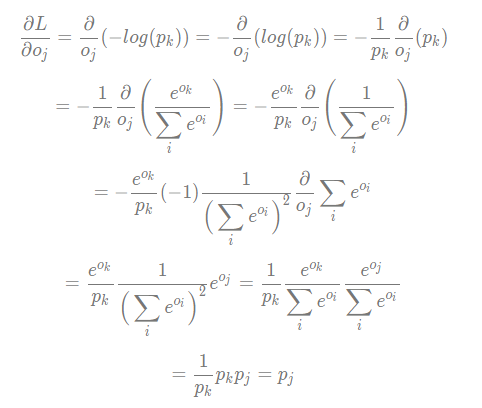
It means

As to example above, the gradient of cross entropy loss function is:

If you want to know how to compute the gradient of softmax function, you can read:
Understand Softmax Function Gradient: A Beginner Guide – Deep Learning Tutorial